Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
Support Vector Machine (SVM) is primarily a classier method that performs classification tasks by constructing hyperplanes in a multidimensional space that separates cases of different class labels. SVM supports both regression and classification tasks and can handle multiple continuous and categorical variables. For categorical variables a dummy variable is created with case values as either 0 or 1. Thus, a categorical dependent variable consisting of three levels, say (A, B, C), is represented by a set of three dummy variables:
A: {1 0 0}, B: {0 1 0}, C: {0 0 1}
The advantages of support vector machines are:
- Effective in high dimensional spaces.
- Still effective in cases where number of dimensions is greater than the number of samples.
- Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
- Versatile: different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.
The disadvantages of support vector machines include:
- If the number of features is much greater than the number of samples, the method is likely to give poor performances.
- SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation.
- Requires full labeling of input data
- The SVM is only directly applicable for two-class tasks. Therefore, algorithms that reduce the multi-class task to several binary problems have to be applied; see the multi-class SVM section.
- Parameters of a solved model are difficult to interpret.
- Uncalibrated class membership probabilities
To construct an optimal hyperplane, SVM employs an iterative training algorithm, which is used to minimize an error function. According to the form of the error function, SVM models can be classified into four distinct groups:
- Classification SVM Type 1 (also known as C-SVM classification)
- Classification SVM Type 2 (also known as nu-SVM classification)
- Regression SVM Type 1 (also known as epsilon-SVM regression)
- Regression SVM Type 2 (also known as nu-SVM regression)
Classification SVM
CLASSIFICATION SVM TYPE 1
For this type of SVM, training involves the minimization of the error function:
subject to the constraints:
where C is the capacity constant, w is the vector of coefficients, b is a constant, and  represents parameters for handling nonseparable data (inputs). The index i labels the N training cases. Note that
represents parameters for handling nonseparable data (inputs). The index i labels the N training cases. Note that  represents the class labels and xi represents the independent variables. The kernel
represents the class labels and xi represents the independent variables. The kernel  is used to transform data from the input (independent) to the feature space. It should be noted that the larger the C, the more the error is penalized. Thus, C should be chosen with care to avoid over fitting.
is used to transform data from the input (independent) to the feature space. It should be noted that the larger the C, the more the error is penalized. Thus, C should be chosen with care to avoid over fitting.
CLASSIFICATION SVM TYPE 2
In contrast to Classification SVM Type 1, the Classification SVM Type 2 model minimizes the error function:
subject to the constraints:
In a regression SVM, you have to estimate the functional dependence of the dependent variable y on a set of independent variables x. It assumes, like other regression problems, that the relationship between the independent and dependent variables is given by a deterministic function f plus the addition of some additive noise:
Regression SVM
y = f(x) + noise
The task is then to find a functional form for f that can correctly predict new cases that the SVM has not been presented with before. This can be achieved by training the SVM model on a sample set, i.e., training set, a process that involves, like classification (see above), the sequential optimization of an error function. Depending on the definition of this error function, two types of SVM models can be recognized:
REGRESSION SVM TYPE 1
For this type of SVM the error function is:
which we minimize subject to:
REGRESSION SVM TYPE 2
For this SVM model, the error function is given by:
which we minimize subject to:
There are number of kernels that can be used in Support Vector Machines models. These include linear, polynomial, radial basis function (RBF) and sigmoid:
Kernel Functions
where 
that is, the kernel function, represents a dot product of input data points mapped into the higher dimensional feature space by transformation 
Gamma is an adjustable parameter of certain kernel functions.
The RBF is by far the most popular choice of kernel types used in Support Vector Machines. This is mainly because of their localized and finite responses across the entire range of the real x-axis.
Modern methods
Recent algorithms for finding the SVM classifier include sub-gradient descent and coordinate descent. Both techniques have proven to offer significant advantages over the traditional approach when dealing with large, sparse datasets—sub-gradient methods are especially efficient when there are many training examples, and coordinate descent when the dimension of the feature space is high.
Sub-gradient descent[edit]
Sub-gradient descent algorithms for the SVM work directly with the expression
Note that 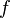 is a convex function of
is a convex function of  and
and  . As such, traditional gradient descent (or SGD) methods can be adapted, where instead of taking a step in the direction of the functions gradient, a step is taken in the direction of a vector selected from the function's sub-gradient. This approach has the advantage that, for certain implementations, the number of iterations does not scale with
. As such, traditional gradient descent (or SGD) methods can be adapted, where instead of taking a step in the direction of the functions gradient, a step is taken in the direction of a vector selected from the function's sub-gradient. This approach has the advantage that, for certain implementations, the number of iterations does not scale with  , the number of data points.[8]
, the number of data points.[8]
 is a convex function of
is a convex function of  and
and  . As such, traditional gradient descent (or SGD) methods can be adapted, where instead of taking a step in the direction of the functions gradient, a step is taken in the direction of a vector selected from the function's sub-gradient. This approach has the advantage that, for certain implementations, the number of iterations does not scale with
. As such, traditional gradient descent (or SGD) methods can be adapted, where instead of taking a step in the direction of the functions gradient, a step is taken in the direction of a vector selected from the function's sub-gradient. This approach has the advantage that, for certain implementations, the number of iterations does not scale with  , the number of data points.[8]
, the number of data points.[8]Coordinate descent[edit]
Coordinate descent algorithms for the SVM work from the dual problem

For each  , iteratively, the coefficient
, iteratively, the coefficient  is adjusted in the direction of
is adjusted in the direction of  . Then, the resulting vector of coefficients
. Then, the resulting vector of coefficients  is projected onto the nearest vector of coefficients that satisfies the given constraints. (Typically Euclidean distances are used.) The process is then repeated until a near-optimal vector of coefficients is obtained. The resulting algorithm is extremely fast in practice, although few performance guarantees have been proved.
is projected onto the nearest vector of coefficients that satisfies the given constraints. (Typically Euclidean distances are used.) The process is then repeated until a near-optimal vector of coefficients is obtained. The resulting algorithm is extremely fast in practice, although few performance guarantees have been proved.
 , iteratively, the coefficient
, iteratively, the coefficient  is adjusted in the direction of
is adjusted in the direction of  . Then, the resulting vector of coefficients
. Then, the resulting vector of coefficients  is projected onto the nearest vector of coefficients that satisfies the given constraints. (Typically Euclidean distances are used.) The process is then repeated until a near-optimal vector of coefficients is obtained. The resulting algorithm is extremely fast in practice, although few performance guarantees have been proved.
is projected onto the nearest vector of coefficients that satisfies the given constraints. (Typically Euclidean distances are used.) The process is then repeated until a near-optimal vector of coefficients is obtained. The resulting algorithm is extremely fast in practice, although few performance guarantees have been proved.
Source:Dell,wikipedia

![f(\vec w, b) = \left[\frac 1 n \sum_{i=1}^n \max\left(0, 1 - y_i(w\cdot x_i + b)\right) \right] + \lambda\lVert w \rVert^2.](https://upload.wikimedia.org/math/9/3/f/93f601213e4d6028c48cf7b218fc3b52.png)

0 Comments:
Post a Comment